... this page is part of the Web Site of George North ...
George North, ,
Homework Assignment # 2
due Friday, September 25, 1995
by: George North
439-68-5643
Computational Geometry
CSCI 6640
Fall 1995
Dr. N. Adla A. DePano
Homework Assignment # 2
(Exercise No. 3 on p. 75 of O'Rourke's text)
1. Min supporting line (Modayur 1991). Design an algorithm to find a line L that
a. has all the points of a given set to one side,
b. minimizes the sum of the perpendicular distances of the points to L.
Assume a hull algorithm is available.
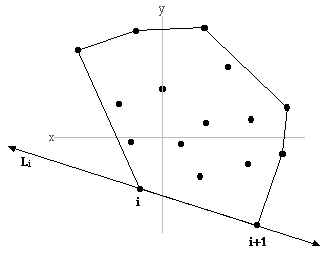
Exists an algorithm that computes the convex hull ( H ) of a set of points ( S) , returning an order (counter clockwise) list of points ( h ) on the hull.
Algorithm : Minimum supporting line - L min
For i = 1 to h-1 (points on hull H less 1)
Make line L i passing through points i and i+1 (a supporting line of S )
For j = 1 to s (points in S )
Sum perpendicular distance from S j to L i (each point in S to line L i )
Remember L min (the line with minimum sum of perpendicular distances) (Exercise No. 6 on p. 75 of O'Rourke's text)
2. Minimum area, convex. Prove characterization 9 of Section 3.1: the minimum area convex polygon enclosing a set of points is the convex hull of the points.
Characterization 9: The convex hull of a set of points S in the plane is the enclosing convex polygon P with smallest area.
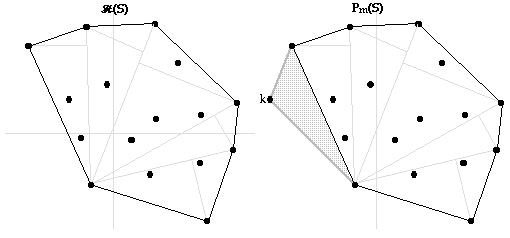
Let H (S) be the convex hull of S .
Characterization 8: the convex hull of a set of points S in the plane is the smallest convex polygon P that encloses S (the convex hull is a convex polygon).
From Characterization 8, we know ...
1. H (S) is a convex polygon.
2. H (S) is the smallest convex polygon that encloses S .
3. Using k , apoint exterior to S, other convex polygons P m (S) can be constructed that contain S.
4. H (S) is smaller than any P m (S) , because P m (S) would contain at least one more triangle than H (S) making its area larger than H (S) .
5. The area of H (S) is smaller than the area of any P m (S) . **
6. H (S) is the enclosing convex polygon with smallest area.
** If h is the number of points on H (S) , exactly h-2 triangles can be constructed by connecting any one point to all other points. The area of H (S) is the sum of the areas of these triangles. The area of any polygon P m (S) can be calculated in a similar manner. Since every P m (S) is composed of at least one point exterior to S, then the area of any P m (S) will be larger that the area of H (S) . 3. In reference to No. 2 above, can we use the concept of perimeter as well, i.e. , convex hull being the polygon containing the given set of points with the smallest perimeter?
Yes. At least two edges of any P m (S) will be longer than the similar edges of H (S) . H (S) is the enclosing convex polygon of S with the smallest perimeter.
(Exercise No. 7 on p. 75 of O'Rourke's text)
4. Minimum area, non convex [easy]. Show by explicit example that the minimum area polygon (perhaps non convex) enclosing a set of points might not be the convex hull of the points.

Given identical sets of points, it is clearly possible that the area of the Convex Hull is not the minimal area of all enclosing polygons
(Exercise No. 1 on p. 80 of O'Rourke's text)
5. Best case? Find the best case for the gift wrapping algorithm (Algorithm 3.3): sets of n points such that the algorithm's asymptotic time complexity is as small as possible as a function of n. What is the time complexity?
The time complexity of the "gift wrap algorithm" is O(n * h) , where n is the total number of points and h is the number of points on the hull. If n = h , complexity is O(n 2 ) , but h may be as small as 3 which will give best case of 3n or O(n) .
(Exercise No. 3 on p. 111 of O'Rourke's text)
6. Diameter and width. Define the diameter of a set of points p 0 , p 1 , ... to be the largest distance between any two points in the set: max i ,j | p i -p j | .
a. Prove that the diameter of a set is achieved by two hull vertices. (by contradiction)
b. A line of support to a set is a line L that touches the hull and has all points on or to one side of L . Prove that the diameter of a set is the same as the maximum distance between parallel lines of support for the set.
c. Two points a and b are called antipodal if the admit parallel lines of support: there are parallel lines of support through a and b . Develop an algorithm for enumerating (listing) all antipodal pairs of a set of points in two dimensions. It helps to view the lines of support as jaws of a caliper. An algorithm can be based on the idea of rotation the caliper around the set.
d. Define the width as the minimum distance between parallel lines of support. Develop an algorithm for computing the width of a set of points in two dimensions.
6 a. Prove that the diameter of a set is achieved by two hull vertices.
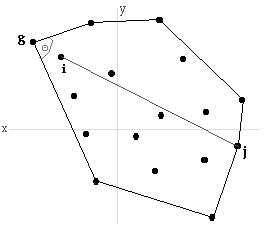
1. Assume that set S of points p 0 , p 1 , ... has a convex hull of set H points h 0 , h 1 , ... . Assume that points i, j is max i,j | p i -p j |, the largest distance between any two points in set S , and assume that point i or point j or both are NOT points on the hull (elements of H ).
2. Point i is NOT on the hull implies that there is a point g, on the hull which forms an angle Q to which i is interior. This means that another line can be formed from point j to point g with length equal to | p g -p j | that is greater than | p i -p j |. | p i -p j | is NOT the largest distance between any two points in set S . This can be shown for a line between any two points when at least one point is not on the hull.
3. Therefore, points i, j is max i,j | p i -p j |, only if i and j are both points in set H , points on the hull of S . 6 b. A line of support to a set is a line L that touches the hull and has all points on or to one side of L . Prove that the diameter of a set is the same as the maximum distance between parallel lines of support for the set.

1. Points a and b are points in S .
2. | a-b | is greater than any other | p i -p j | in S .
3. In question a) above, it was shown that points a and b are on the hull of S .
4. A line drawn through a and perpendicular to line ab is parallel to a line drawn through b and perpendicular to line ab . Both of these lines are lines of support to S .
5. The distance between these lines of support is | a-b |, which is also the diameter of S .
6 c. Two points a and b are called antipodal if they admit parallel lines of support: there are parallel lines of support through a and b . Develop an algorithm for enumerating (listing) all antipodal pairs of a set of points in two dimensions. It helps to view the lines of support as jaws of a caliper. An algorithm can be based on the idea of rotation the caliper around the set.


Exists an ordered set of (at least 3) points H that is the convex hull of S , h is the number on points in H in counter clockwise order.
Algorithm : Antipodal pairs
next p = 3
for i = 1 to h * outer loop executes h times
Line L i is a line of support containing the two points i and i+1
j = next p * next point on hull to check for a parallel line of support
loop * inner loop will execute maximum 2h times
make line P j is parallel to line L i passing through point j
if (line P j is a line of support at point j ) then
* P j is a line of support if it does NOT pass on or within convex angle at point j
Line L i and line Pj are parallel lines of support
SAVE points ( i , j ) and ( i+1, j ) as an Antipodal pairs
exit loop
endif
j = j+1
end loop
next p = j
* t erminates because every point on hull has at least one parallel line of support
end loop
* algorithm will report some duplicate Antipodal pairs
Complexity is O(h), not including finding hull of S. 6 d. Define the width as the minimum distance between parallel lines of support. Develop an algorithm for computing the width of a set of points in two dimensions.
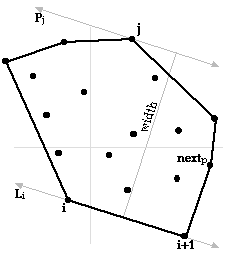
Algorithm in 6c above can be used to obtain the minimum supporting line
Algorithm : Width of convex polygon
W min = "some max value"
next p = 3
for i = 1 to h * outer loop executes h times
Line L i is a line of support containing the two points i and i+1
j = next p * next point on hull to check for a parallel line of support
loop * inner loop will execute maximum 2h times
make line P j is parallel to line L i passing through point j
if (line P j is a line of support at point j) then
Line L i and line Pj are parallel lines of support
calculate W j , length of a line between and perpendicular to L i and P j
if W min > W j then W min = W j * possible width of hull *
exit loop
endif
j = j+1
end loop
* t erminates because every point on hull has at least one parallel line of support
next p = j
end loop
W min = width of hull
Original file name: HW2.rtf
This file was converted with TextToHTML - (c) Logic n.v.