... this page is part of the Web Site of George North ...
Homework Assignment 3
George North, ,
Homework Assignment # 3
due Monday, October 30, 1995
by: George North
439-68-5643
Computational Geometry
CSCI 6640
Fall 1995
Dr. N. Adla A. DePano
(Exercise No. 3 on p. 242 of O'Rourke's text)
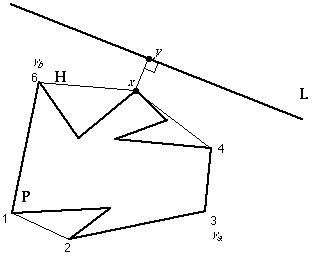
1. Stabbing a convex polygon. Design an algorithm for finding the intersection of a convex polygon P of n vertices with a line L . This is often called called a "stabbing" problem for obvious reasons. Achieve O (log n) time.
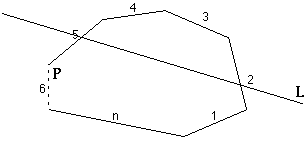
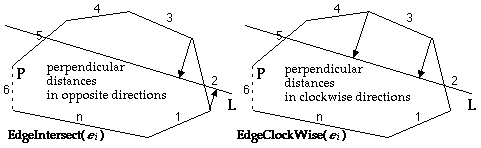
If a line L intersects two edges of convex polygon P then L intersects P . Line L does not intersect P if it touches only 1 vertex. Line L does not intersect P if it touches two consecutive vertexes ( L is on an edge of P ). For the purposes of this algorithm, it will be assumes that a vertex of P belongs to its counter clockwise edge. This allows the algorithm to be defined in terms of edges. Each edge, e , has two vertices, e v1 and e v2 . Line L intersects edge e if perpendicular lines from its vertices to L are in opposite directions. Edge e is cloc k wise of L if perpendicular lines from its vertices to L are in clockwise direction.
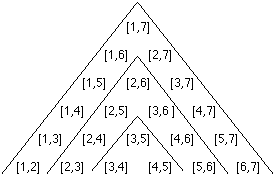
With n vertices, there are also n edges of a convex polygon. If line L intersects P then it intersects two edges of P . So, there are (n-1)! possible combinations of edges that could be intersected by L . An ordered set of these edges can be created as follows:
[1,2], [1,3], ... , [1,n], [2,n], [3,n], ... , [n-1,n]
>> [2,3], [2,4], ... , [2,n-1], [3,n-1], [3,n-1], ... , [n-2,n-1]
>> [3,4], [3,5], ... , [3,n-2], [4,n-2], [4,n-2], ... , [n-3,n-2]
>> ...
for example: n=7
The algorithm will be in two parts.
First , an ordered search is performed of the above set of edge pairs as follows: [1, n], [2, n-1], [3, n-2], ... , [n-n/2, n-((n+1)/2)+1] -- for example, with n = 7: [1,7], [2,6], [3,5]. This search is looking for ONE (at least) edge intersection of L . If both edges of a pair intersect L we are finished. If NO intersection is found in any pair, we are finished -- L does not intersect P .
Second , with one edge intersection found in first step, a divide and conquer search is made of the remaining edges. At this point the remaining edges to search are known, and are an ordered set -- for example, if edge set [2,6] in produced one edge intersectio n (step 1), then the remaining edges to search are: 3, 4, and 5.
The complexity of both first and second part is O (lg n). Algorithm complexity is O (lg n).
continues next page --- (Exercise No. 3 on p. 242 of O'Rourke's text)
1. Continues --
Problem : Convex polygon P is constructed of a counter clockwise set of n edges
E = 1, 2, 3, ... , n . Find the edge pair (i, j) in E that is intersected by a line L .
Algorithm :
Function : EdgeIntersect( e i ), returns TRUE if line L intersects edge i
EdgeClockWise( e i ), returns TRUE if edge i is clockwise to line L
Step1 :
Initialize: i = 1 (1st edge), j= n
Loop
Edges i and j are checked for intersection with L . -- O (1)
If BOTH edges are intersected by L ... FINISHED
If edge j = i + 1, the other edge is j ... FINISHED
If "one edge intersection is found" then
" an ordered list of the remaining possible edges is passed to Step2 "
i = i + 1; j = j - 1;
if i = j then " L does NOT intersect P" ... FINISHED
end Loop
Step 1 --> Complexity = O (lg n)
Note: From step one, we know that line L intersects one of the pair of edges ( i , j ), i < j - 1. Also it is known that the remaining edge intersection is one of the edges from i+1 to j-1.
-- i.e. if L intersects either edge 2 or 6, the remaining possible edges are 3, 4, 5.
i = i + 1; j = j - 1;
Step2:
Loop
k = median edge between i and j -- (j-i)/2
if EdgeIntersect( k ) = true then " k is the other intersected edge" ... FINISHED
if EdgeClockWise( k ) then j = k else i = k
-- each loop interation cuts in half the # of edges left to search
end Loop
Step 2 --> Complexity = O (lg n)
Each iteration in step 1 eliminates half the remaining edges. Step 2 need only look at the edges not processed in Step 1. Each iteration in step 2 eliminates half the remaining edges.
-- > Complexity = O (lg n) (Exercise No. 4 on p. 242 of O'Rourke's text)
2. Line-polygon distance. Design an algorithm to determine the distance between an arbitrary polygon P of n vertices and a query line L . Define the distance to be
min|x-y|:x OE P, y OE P,
x,y
where x and y are points. Try to achieve O (log n ) per query after preprocessing. Remember that the inputs are an arbitrary polygon (not necessarily convex; one can assume that it is simple) and the query lines.
If
line L does not intersect polygon P .
then
min|x-y|:x OE P, y OE P is a line [x,y] from a vertex of P perpendicular to L .
x,y
and
this same vertex will be on the Convex Hull of P .
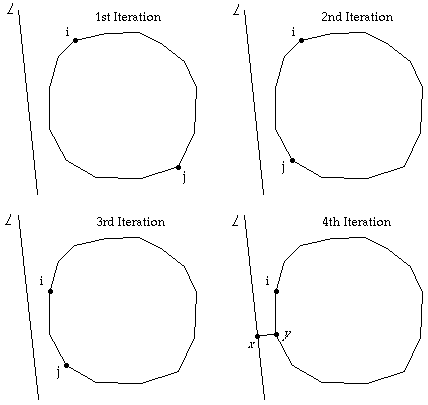
Preprocessing :
1). Find Convex Hull H (of m vertices) of P . H is a counter clockwise ordered set. --> Complexity = O (n lg n)
2). Find one antipodal pair of Hull vertices, v a and v b . These are opposing vertices, and divide H about in half.
--> Complexity = O (n)
Problem : H is the hull of a simple polygon P . H is constructed of a counter clockwise set of n vertices V = 1, 2, 3, ... , n . v a and v b is an antipodal pair on H .
Algorithm :
Initialize : i = v a
j = v b
Loop
calculate perpendicular distance (d i and d j ) to L of vertices i , j --> O (1)
if ( i + 1) = j then "minimum (d i , d j ) is minimum distance to L " ... FINISHED
if d i < d j then "minimum distance vertex lies clockwise of i "
j = median value clockwise of i , j
else "minimum distance vertex lies counter clockwise between i and j"
i = median value counter clockwise of i , j
end Loop
--> Complexity = O (lg n)
Each iteration of Step 1 divides the number of vertices remaining to examine in half.
(Exercise No. 2 on p. 269 of O'Rourke's text)
3. Interval trees. Preprocess a set of n intervals I with integer endpoints so that they can be efficiently queried. Consider three types of queries (the preprocessing need not be the same for all three):
a) Is x in some interval in I
b) Within how many intervals of I does x lie?
c) Does the interval [ r , s ] intersect any interval of I ?
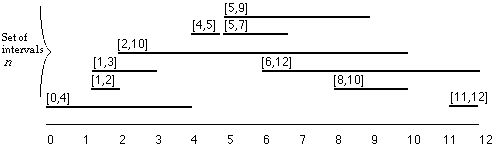
Given : a set of n intervals I ... each interval is a line [ a , b ]. Two approaches will be presented.
Approach I
Preprocessing :
Construct data structure DA , with integer index. DA ( i ) is an integer initialized to 0. For each interval in I , add 1 to each D A ( i ) for a <= i <= b .
loop for each interval [ a , b ] in I
j = a
loop while j <= b
DA ( j ) = DA ( j ) + 1
j = j + 1
end loop
end loop
--> Complexity = O ( n m ) ... where n is the number of intervals, and m is the length of intervals. Length [ a , b ] = | b - a |. This would only be practical when the maximum length of a very large majority of intervals was less than some small value k , so that preprocessing was complexity O ( n k ).
DA ( i ) > 0 if there exist any interval [ a , b ], such that a <= i <= b .
DA ( i ) = "the number of intervals in I that contain integer value i "
Approach I
Algorithm 3a -- Is point x in some interval I
... can be accomplished by checking if DA ( x ) > 0. If x is an integer. If x is a real, then it is necessary to first coerce x to integer.
--> Complexity -- O (1)
Algorithm 3b - Within how many intervals of I does x lie?
... number of intervals in I = DA ( x ) > 0. If x is an integer. If x is a real, then it is necessary to first coerce x to integer.
--> Complexity -- O (1)
Algorithm 3c - Does the interval [ r , s ] intersect any interval of I ?
... can be accomplished by checking if EITHER DA ( r ) > 0 OR DA ( s ) > 0.
- --> Complexity -- O (1)
Approach II
Preprocessing :
Construct an A-V-L tree, A a , ordered such that: O ( n lg n)
i) using the a component of intervals [ a , b ]: left children are less then right children, and ii) equal a components are ordered by length ( | b-a | ), shortest as left child.
Construct an A-V-L tree, A b , ordered such that: O ( n lg n)
i) using the b component of intervals [ a , b ]: left children are less then right children, and ii) equal b components are ordered by length ( | b-a | ), shortest as left child.
NOTE: an A-V-L tree is a balanced binary tree with search complexity of O ( lg n).
Approach II
Functions:
Search_a( x ) : ... binary search (i.e. using recursion) A a tree comparing x to a components, return(TRUE) if a >= x <= b, else return(FALSE).
--> Complexity = O (lg n)
Search_b( x ) : ... binary search (i.e. using recursion) A b tree comparing x to b components, return(TRUE) if b <= x >= a, else return(FALSE).
--> Complexity = O (lg n)
isIn( x ) : ... return(TRUE) if either Search_a( x ) or Search_b( x ) returns true, else return(FALSE).
--> Complexity = O (lg n)
Algorithm 3a -- Is point x in some interval I
... can be accomplished by using function : isIn( x )
--> Complexity -- O (lg n)
Algorithm 3b - Within how many intervals of I does x lie?
... can be accomplished by searching every interval in I for a >= x <= b, and counting the number of matches.
--> Complexity -- O (n)
Algorithm 3c - Does the interval [ r , s ] intersect any interval of I ?
... can be accomplished by using function : isIn( x ) --
return(TRUE) if isIN( r ) or if isIN( s );
- --> Complexity -- O (lg n)
Approach II, Algorithm 3b with complexity of O (n) needs improvement. Approach I would be preferred if repeated calls were expected to Algorithm 3b. When the number of calls to Algorithm 3b nears n , the number of intervals ... then Approach I would provide better performance. Approach I would be practical when the maximum length of a very large majority of intervals was less than some small value k , so that preprocessing was complexity O ( n k ) ... and the number of calls to Algorithm 3b was greater than k. (Exercise No. 3 on p. 111 of O'Rourke's text)
4. Consider the set of regular n -gons. (The regular 3-gon is the equilateral triangle, the regular 4-gon is the square, etc.] Investigate the complexity of answering the following type of query: Given a regular n -gon R n , is the point p inside R n ? The limiting shape for regular n-gons as n grows without bound is a circle. Show that the complexity of answering such a query for a circle is O (1).
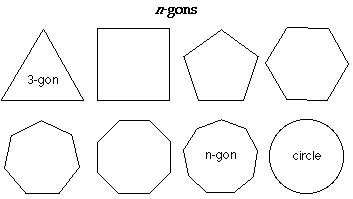
1. As seen in class, O (1) time is required for point location in a triangle.
2. As seen in class, O (n) time is required for point location in a n-gon.
3. Point location inside a circle can be done in O (1) time -- i.e. is the distance to point p from center of circle > it radius?
As n approaches infinity, an n-gon is a circle. From 1. and 2. above, it could be assumed that complexity for a circle would also be infinity. --> ??????
Original file name: HW3rtf
This file was converted with TextToHTML - (c) Logic n.v.