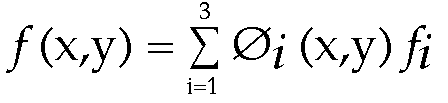... this page is part of the Web Site of George North ...
Geophysical parametrization
and interpolation of irregular data using
Natural Neighbours
(Malcolm Sambridge, Jean Braun and Herbert McQueen)
CSCI 6640, Fall 1995
December 2, 1995
A summary by:
George North
Geophysical parametrization and interpolation of irregular data using Natural
Neighbours
by:
Malcom Sambridge, Jean Braun, and Herbert McQueen ---- November, 1994
Summary

1. Their method makes use of powerful algorithms from computational geometry.
2. Using 'Delaunay' triangles (2-D) and tetrahedra (3-D)
3. "Interpolating" a property of Earth. e.g. temperature, seismic
velocity. Interpolating is to estimate a value of (a function or series)
between two known values.
4. Smooth interpolating anywhere in the medium by using Natural Neighbour
Interpolation .
5. Advantages of this method are:
the original function values are recovered exactly at reference points.
interpolation is entirely local (a point is influenced by its natural neighbour
nodes).
it is ideally suited for irregularly spaced, arbitrary, geophysical data.
Applications

1. Geophysics relies on methods of parameterization and interpolation.
2. Examples include:
Modeling of mantle convection
Crustal deformation
Thermal conduction/advection
Interpolation of topography
" of gravity
" of magnetic fields
Estimating seismic velocity
3. Algorithms from Computational Geometry
are new to geophysics
earliest use is said to be 1987
are growing rapidly
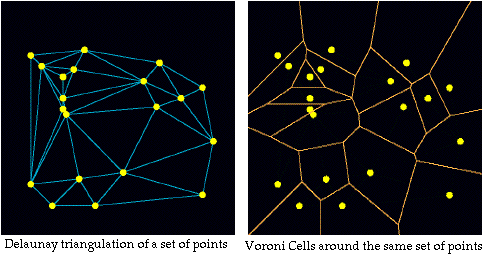
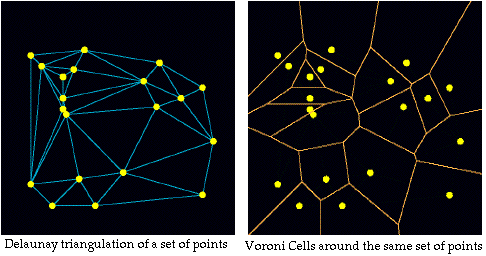
Delaunay Triangles

Delaunay Triangles are the dual of Voronoi cells (diagrams) -- if one is
known, the other is completely known
" " are the "best looking" set of triangles
" " the set of 'least long and thin' triangles
" " referred to as the maximum-minimum angle property
" " strongly determine the density of nodal distribution ... Voronoi
cells are an inverse measure of nodal density.
Natural Neighbours

1. Trees in a forest mature into a pattern that CANNOT be attributed
to haphazard dropping of seeds.
2. Giant's Causeway in northern Ireland ...
3. Dried Lake-bed in northern Chile
4. Math has idealized this as ... natural neighbors
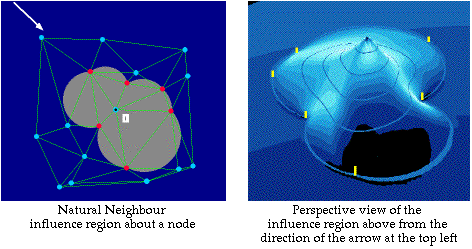
Natural Neighbour nodes

Natural Neighbour nodes are a set of 'nearby' surrounding nodes
" " (s) of any node are those in the neighbouring Voronoi cells
" " (s) of any node are those to which the node is connected by
the sides of Delaunay triangles.
Natural Neighbors Interpolation

1. Important property interpolated value at any point has the useful property
of being exactly equal to the original function value at the nodes, i.e.
f (xi) = f i
2. " " interpolation is a purely local procedure ... each node
i only influences the region around it
3. " " the interpolated function is continuously differentiable
everywhere except at the nodes ... its smoothness is attributed to the smoothness
of a natural neighbour surface
4. " " these hold for any dimension
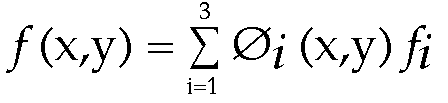
we will skip the MATH
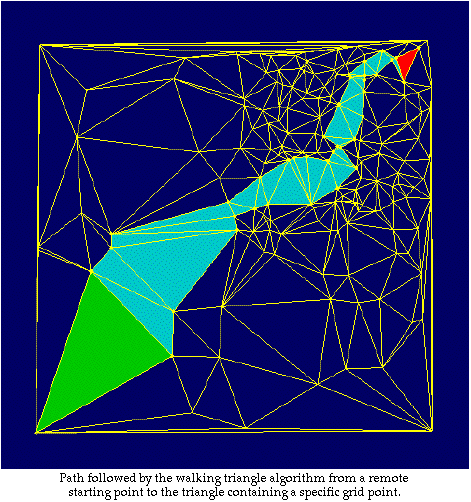
Walking Triangle