... this page is part of the Web Site of George North ...

---

Homework Supplement

Point Location





by: George North
439-68-5643

Computational Geometry
CSCI 6640
Fall 1995
Instructor: Dr. N. Adlai A. DePano TABLE OF CONTENTS



Review -- Geophysical parametrization 3
Planar Point Location Bibliography 6
Geophysical parametrization and interpolation of irregular data using natural neighbours -- by: Malcom Sambridge, Jean Braun,
and Herbert McQueen 13
Geophysical parametrization and interpolation of irregular data using natural neighbours

by:
Malcom Sambridge, Jean Braun, and Herbert McQueen,



A SUMMARY by: George North

In searching the Internet for a paper on which to base this report, I found a site "Geometry in Action."
(http://www.ics.uci.edu/~eppstein/geom.html).
Its purpose is to present various areas in which ideas from computation geometry are used to solve real world problems. Information regarding many areas are presented (with links) including: architecture, astronomy, cartography, geographic information systems, computer aided design, computer aided manufacturing, constraint solving, data mining and multidimensional analysis, graph drawing, computer graphics, interpolation, medical imaging, mesh generation, metrology, molecular modeling and nanotechnology, origami, robot motion planning, signal processing, textile layout, typography, video game programming, computer vision, VLSI design, Voronoi diagrams, windowing systems. It was interesting browsing these many sites. The paper I chose, like most, is very technical in its presentation. Admittedly, I cannot follow many of its topics. Please note that the graphics included here are borrowed from the above mentioned web pages.


A goal of Geophysical parametrization is the estimation of mineral reserves in a deposit using information obtained from bore holes and modeling crack patterns in basalt due to contraction on cooling. Interpolation is to estimate a value of (a function or series) between two known values. Extrapolation is to estimate (a value of a variable outside a known range) from values within a known range by assuming that the estimated value follows logically from the known values. 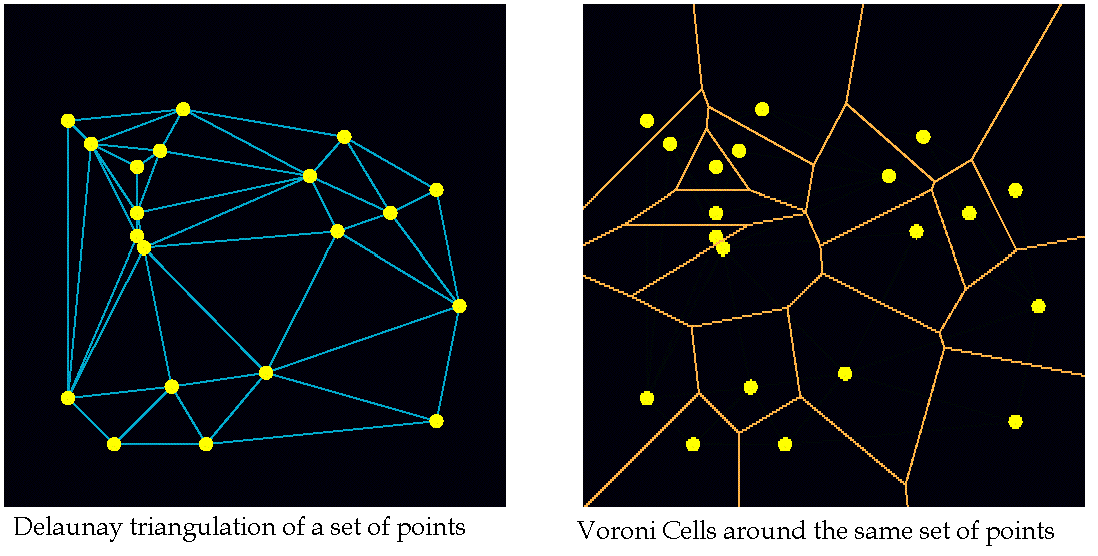The natural neighbours (clearly British) of any node are those in the neighbouring Voronoi cells, or equivalently, those to which the node is connected by the sides of Delaunay triangles (see cover graphic).

A Voronoi diagram of a set of "sites" (points) is a collection of regions that divide up the plane. Each region corresponds to one of the sites, and all the points in one region are closer to the corresponding site than to any other site. All of the Voronoi regions are convex polygons. Some of them are infinite -- these correspond to the sites on the convex hull. The boundary between two adjacent regions is a line segment, and the line that contains it is the perpendicular bisector of the segment joining the two sites. Usually, Voronoi regions meet three at at time at Voronoi points. If three sites determine Voronoi regions that meet at a Voronoi point, the circle through those three sites is centered at that Voronoi point, and there are no other sites in the circle. The Delaunay triangulation is the dual of the Voronoi diagram. To build the Delaunay triangulation, draw a line segment between any two sites whose Voronoi regions share an edge. This procedure splits the convex hull of the sites into triangles. Please see cover graphic for example.

The interpolating property of the Earth's crust make the procedures presented in this paper ideally suited for gridding irregularly spaced geophysical data. Natural neighbour interpolation describes a unique set of nodes that define the 'neighourhood' of a point in the plane. A set of nautural neighbours reflect the distance between nodes when their distance is relatively large in some part and when the distribution is highly anisotropic (having properties that differ according to the direction of measurement). The size and shape of the region that can influence any point will adapt naturally to the local variation in node density. Natural neighbour interpolation uses the areas of Voronoi cells to determine these weights.

Two examples are presented to demonstrate the power of this technique: i) Combining Global and regional scale models on a sphere; and ii) From subduction zones to spherical harmonic models of the Mantle . With this approach is is possible to build 2-D and 3-D with an enormous variation in cell sizes and complex geometry. Fine detail may be imposed anywhere by simply adding more nodes locally and letting the Delaunay tessellation (form a mosaic pattern) produce the cells. Also presented is an algorithm, called "walking triangle," used to find the triangle containing a given point.



Planar Point Location -- Bibliography (1986 - 1995)

@inproceedings{acg-cdctd-87
author = M. J. Atallah and R. Cole and M. T. Goodrich"
title = Cascading divide-and-conquer: {A technique for designing parallel algorithms"
booktitle = Proc. 28th Annu. IEEE Sympos. Found. Comput. Sci."
year = 1987
pages = 151--160"
keywords = cascading divide-and-conquer algorithm parallel algorithms concurrent-read- exclusive-write parallel random-access machine"
precedes = acg-cdctd-89"
annote = Triangulation of a polygon using $O(\log n)$ time and
$O(n)$ processors."
abstract = Techniques are presented for parallel
divide-and-conquer resulting in improved parallel
algorithms for a number of problems including
intersection detection trapezoidal decomposition
(hence polygon triangulation) and planar point
location (hence Voronoi diagram construction).
Efficient parallel algorithms are also given for
fractional cascading three-dimensional maxima two-set dominance counting and visibility from a point. All of the algorithms run in O(log n) time with either a linear or sublinear number of processors in the
concurrent-read- exclusive-write parallel random-access machine model. 20 refs."


@article{cj-nrdpp-92
author = S. W. Cheng and R. Janardan"
title = New results on dynamic planar point location"
journal = SIAM J. Comput."
volume = 21
year = 1992
pages = 972--999"
keywords = point location dynamization"


@inproceedings{cpt-uadpl-93
author = Y.-J. Chiang and F. P. Preparata and R. Tamassia"
title = A Unified Approach to Dynamic Point Location Ray Shooting and Shortest Paths in Planar Maps"
booktitle = Proc. 4th ACM-SIAM Sympos. Discrete Algorithms"
year = 1993
pages = 44--53"
update = 93.05 smid"


@inproceedings{ct-dtmpp-91
author = Y.-J. Chiang and R. Tamassia"
title = Dynamization of the trapezoid method for planar point location"
booktitle = Proc. 7th Annu. ACM Sympos. Comput. Geom."
year = 1991
pages = 61--70"
keywords = point location subdivision dynamizing data structures"
precedes = ct-dtmpp-92"


@article{ct-dtmpp-92
author = Y.-J. Chiang and R. Tamassia"
title = Dynamization of the trapezoid method for planar point location in monotone subdivision"
journal = Internat. J. Comput. Geom. Appl."
volume = 2
number = 3
year = 1992
pages = 311--333"
keywords = planar point location dynamic data structures monotone subdivision analysis of algorithm"
succeeds = ct-dtmpp-91"


@article{cz-opabd-90
author = R. Cole and O. Zajicek"
title = An optimal parallel algorithm for building a data structure for planar point location"
journal = J. Parallel Distrib. Comput."
volume = 8
year = 1990
pages = 280--285"
update = 93.05 devillers"


@article{lp-pbppl-89
author = D. T. Lee and F. P. Preparata"
title = Parallel batched planar point location on the {CCC "
journal = Inform. Process. Lett."
volume = 33
year = 1989
pages = 175--179"
update = 93.05 devillers"


@article{p-pplr-90
author = F. P. Preparata"
title = Planar point location revisited"
journal = Internat. J. Found. Comput. Sci."
,@techreport{pt-fdppl-87
author = F. P. Preparata and R. Tamassia"
title = A fully dynamic planar point location technique"
type = Report"
number = UILU-ENG-87-2266"
institution = Coordinated Sci. Lab. Univ. Illinois"
address = Urbana IL"
year = 1987
keywords = point location data structuring on-line"
precedes = pt-dpplo-89"


@inproceedings{pt-dpplo-89
author = F. P. Preparata and R. Tamassia"
title = Dynamic planar point location with optimal query time"
booktitle = Proc. 6th Sympos. Theoret. Aspects Comput. Sci."
series = Lecture Notes in Computer Science"
volume = 349
publisher = Springer-Verlag"
year = 1989
pages = 84--95"
keywords = subdivisions point location on-line two-dimensional"
succeeds = pt-fdppl-87"
precedes = pt-dpplo-90"


@article{pt-dpplo-90
author = F. P. Preparata and R. Tamassia"
title = Dynamic planar point location with optimal query time"
journal = Theoret. Comput. Sci."
volume = 74
year = 1990
pages = 95--114"
succeeds = pt-dpplo-89"

@inproceedings{pt-fdtpl-88
author = F. P. Preparata and R. Tamassia"
title = Fully dynamic techniques for point location and transitive closure in planar structures"
booktitle = Proc. 29th Annu. IEEE Sympos. Found. Comput. Sci."
year = 1988
pages = 558--567"
comments = In two journal papers: \cite{tp-dmpda-90 ,
\cite{pt-fdplm-89 "


@inproceedings{rs-orpac-87
author = John H. Reif and Sandeep Sen"
title = Optimal Randomized Parallel Algorithms For Computational Geometry"
booktitle = Proceedings of the 1987 International Conference on Parallel Processing."
publisher = Pennsylvania State Univ Press"
address = University Park PA"
year = 1987
pages = 270--277"
keywords = randomized parallel algorithms computational geometry concurrent-read exclusive write parallel random-access machines"
annote = Including polygon triangulation."
abstract = The authors present parallel algorithms for some
fundamental problems in computational geometry which
have optimal running time with very high probability
(approaching 1 as n yields infinity). These include
planar point location triangulation trapezoidal
decomposition 3-D maxima two- set dominance counting, and range-counting among others. Most of these algorithms run on the CREW PRAM model with O(n)
processors and execute in O(log n) time. Most of these
algorithms use a novel data structure called the nested plane sweep tree. Random splitting is used very
effectively to divide and conquer on the plane raising the possibility of extending this technique to higher dimensions. 20 refs."


@article{rs-orpac-92
author = John H. Reif and Sandeep Sen"
title = Optimal Randomized Parallel Algorithms For Computational Geometry"
journal = Algorithmica"
volume = 7
number = 1
year = 1992
pages = 91--117"
keywords = randomized algorithms parallel algorithms crew pram computational geometry"
update = 93.09 rote"
abstract = We present parallel algorithms for some fundamental
problems in computational geometry which have a running time of O(log n) using n processors with very high probability (approaching 1 as n yields infinity ). These include planar-point location triangulation and trapezoidal decomposition. We also present optimal
algorithms for three-dimensional maxima and two-set
dominance counting by an application of integer
sorting. Most of these algorithms run on a CREW PRAM
model and have optimal processor-time product which
improve on the previously best-known algorithms of
Atallah and Goodrich [5] for these problems. The crux
of these algorithms is a useful data structure which
emulates the plane- sweeping paradigm used for
sequential algorithms. We extend some of the techniques used by Reischuk [26] and Reif and Valiant [25] for flashso@article{st-pplps-86
author = N. Sarnak and R. E. Tarjan"
title = Planar point location using persistent search trees"
journal = Commun. ACM"
volume = 29
year = 1986
pages = 669--679"


@article{s-facdt-87
author = S. W. Sloan"
title = A fast algorithm for constructing {Delaunay triangulations in the plane"
journal = Advances in Engineering Software"
volume = 9
number = 1
month = jan
year = 1987
pages = 34--55"
annote = Your basic incremental switching algorithm. Points are
sorted into bins to increase speed of point location
(which walks the triangulation starting at the
previous triangle.)"
abstract = The primary purpose of the paper is to present a
FORTRAN 77 code for the efficient triangulation of
planar data points as might be required for the mesh
generation of a finite element analysis. The author
describes in detail the various features of the
algorithm and compares them to existing routines. The
efficiency of the algorithm is demonstrated for
randomly distributed data points where the number of
points varies between 100 and 10,000. It is shown that
the proposed scheme outperforms existing routines for
both large and small data sets. -G. E. Bell St.
Andrews U"


@article{t-irmdp-91
author = R. Tamassia"
title = An incremental reconstruction method for dynamic planar point location"
journal = Inform. Process. Lett."
volume = 37
year = 1991
pages = 79--83"
keywords = point location triangulation computational geometry planar point location"
abstract = We present a fully dynamic technique for point
location in triangulations that allows a tradeoff
between query and update time and can be used in
conjunction with any of the known static point location data structures. Let $S$ be a triangulation whose current number of vertices is $n$. We show that for any smooth nondecreasing integer function $b(n)$ with $2\le b(n) \le \sqrt n$ there exists a dynamic point location data structure for $S$ with space $O(n)$, query time $O((\log^2n)/\log b(n))$ and update time $O((\log^2n)b(n)/\log b(n))$. (Author abstract) 15 Refs."

@inproceedings{tv-opatc-89
author = R. Tamassia and J. S. Vitter"
title = Optimal Parallel Algorithms for Transitive Closure and Point Location in Planar Structures"
booktitle = Proc. ACM Sympos. Parallel Algorithms Architect."
year = 1989
pages = 399--408"
keywords = graph drawing"
update = 93.09 tamassia"